Методические аспекты изучения линий второго порядка в школьном курсе алгебры 7-9 классов

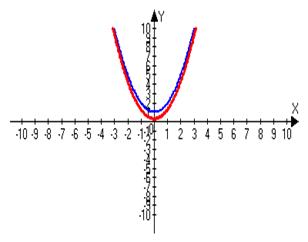
Рис. 1 - График функции

Теперь учащиеся по коэффициентам квадратного трехчлена могут представить общий вид соответствующей параболы и вычислить координаты её вершины, путём выделения полного квадрата в данном трёхчлене. В результате выполнения практических заданий, на построение графика квадратичной функции необходимо в строгой последовательности проговорить и зафиксировать алгоритм построения функции .

В системе упражнений, учебников по алгебре, значительное место отводится задачам прикладного характера. Завершается тема рассмотрением вопроса о решении квадратных неравенств, выбор решения основан на использовании графиков.

При работе с теоретической частью и выполнении заданий учащиеся должны будут проводить наблюдение, выдвигать гипотезы, рассуждать, доказывать, переходить от одной системы терминов к другой.

Затем отмечается, что график любой квадратичной функции - это парабола и приведены различные виды парабол.

В восьмом классе идет изучение функции, изложение материала начинается с анализа примеров реальных зависимостей. Учащимся предлагается рассмотреть зависимость времени движения пешехода от его скорости, длины стороны прямоугольника заданной площади от длины другой его стороны, количества товара, которое можно купить на определенную сумму денег, от цены этого товара. Обобщая эти примеры постепенно приходим к определению функции (называемой обратной пропорциональностью).

Все свойства и график функции в учебнике рассматриваются на примере конкретных функций (Например, ). По точкам строится график данной функции и вводится его название (гипербола). Здесь из свойств выделяются только область определения, промежутки убывания и возрастания функции и делается замечание, что график данной функции не пересекает координатные оси. Исследование проводится подробно для первого случая, когда , а для второго случая ( ) приведены только конечные выводы и результаты.

Традиционно построение графика обратной пропорциональности вызывает у учащихся трудности. Многие строят его небрежно, не соблюдая симметрии ветвей, ветви бывают очень короткие, очень часто в работах учащихся одна из ветвей гиперболы сначала приближается, например, к оси х, а затем удаляется от нее. Для предупреждения подобных ошибок очень важно проанализировать особенности графика, обратив внимание учащихся на то, что график состоит из двух ветвей, симметричных друг другу относительно начала координат. Каждая ветвь гиперболы по мере удаления от начала координат становится все ближе и ближе к осям, но не пересекает их. Бесконечное приближение ветвей к осям координат можно проиллюстрировать в ходе небольшого числового опыта: например, подставить в формулу вместо х несколько достаточно больших чисел в порядке их возрастания и понаблюдать, как изменяется при этом значение .

Еще о педагогике:

Исторический смысл гуманистической педагогики
Смысл изменения системы воспитания - в ее гуманизации, когда в совершенствовании человека видят не средство благополучия общества, а цель общественной жизни, когда становление личности предполагает выявление и совершенствование всех сущностных сил человека. Гуманистическое воспитание, предстоит утв ...

Работа за компьютером с помощью меню
При работе с программой пользователю часто бывает необходимо подать ей определенную команду, выбрать необходимый режим работы или осуществить какое-либо действие. Для передачи команд программе графический пользовательский интерфейс включает систему меню и панелей инструментов. Меню - это набор пунк ...

Метод проектов в начальной школе
Метод проектов можно представить как способ организации педагогического процесса, основанный на взаимодействии педагога и ученика, способ взаимодействия с окружающей средой, поэтапная практическая деятельность по достижению поставленной цели. В настоящее время можно заметить, что как в теории, так ...